Làm nên lịch sử với con số có 42 chữ số
Một bí ẩn toán học kéo dài hàng thập niên đã được giải mã bởi các nhà khoa học tại Đại học Paderborn và KU Leuven bằng cách sử dụng số Dedekind thứ 9. Từ năm 1991, các chuyên gia trên toàn thế giới đã tiến hành tìm kiếm giá trị này. Với sự trợ giúp của siêu máy tính Noctua, các nhà khoa học Paderborn đã tạo dãy số chính xác. Hội thảo quốc tế về hàm Boolean và ứng dụng của chúng (BFA) được tổ chức tại Na Uy vào tháng 9 sẽ trình bày kết quả.
Dự án luận văn thạc sĩ của Lennart Van Hirtum (người trước đó là sinh viên khoa học máy tính tại KU Leuven và hiện là cộng tác viên nghiên cứu tại Đại học Paderborn) đã đạt được thành công lớn. Các nhà khoa học tham gia nối tiếp một công trình nổi bật: Những con số trước đó trong dãy số Dedekind được tìm thấy bởi chính nhà toán học Richard Dedekind khi ông xác định vấn đề vào năm 1897, và sau đó là những bộ óc vĩ đại trong khoa học máy tính thời kỳ đầu như Randolph Church và Morgan Ward. Van Hirtum nói: "Trong 32 năm, việc tính toán D là một thách thức để ngỏ và người ta đặt câu hỏi liệu có bao giờ có thể tính được con số này hay không."
Cray 2, siêu máy tính mạnh nhất vào thời điểm đó, đã được sử dụng để xác định số trước đó trong dãy số Dedekind, tức là số Dedekind thứ 8, được phát hiện vào năm 1991. Van Hirtum, cùng với những người hướng dẫn luận văn thạc sĩ tại Đại học quốc gia Anh, giải thích động lực của dự án đầy tham vọng khi nó được dự định thực hiện: "Chúng tôi bấy giờ đã hình dung được rằng mình có thể tính được số thứ 9 trên một siêu máy tính lớn."
Hạt cát, cờ vua và siêu máy tính
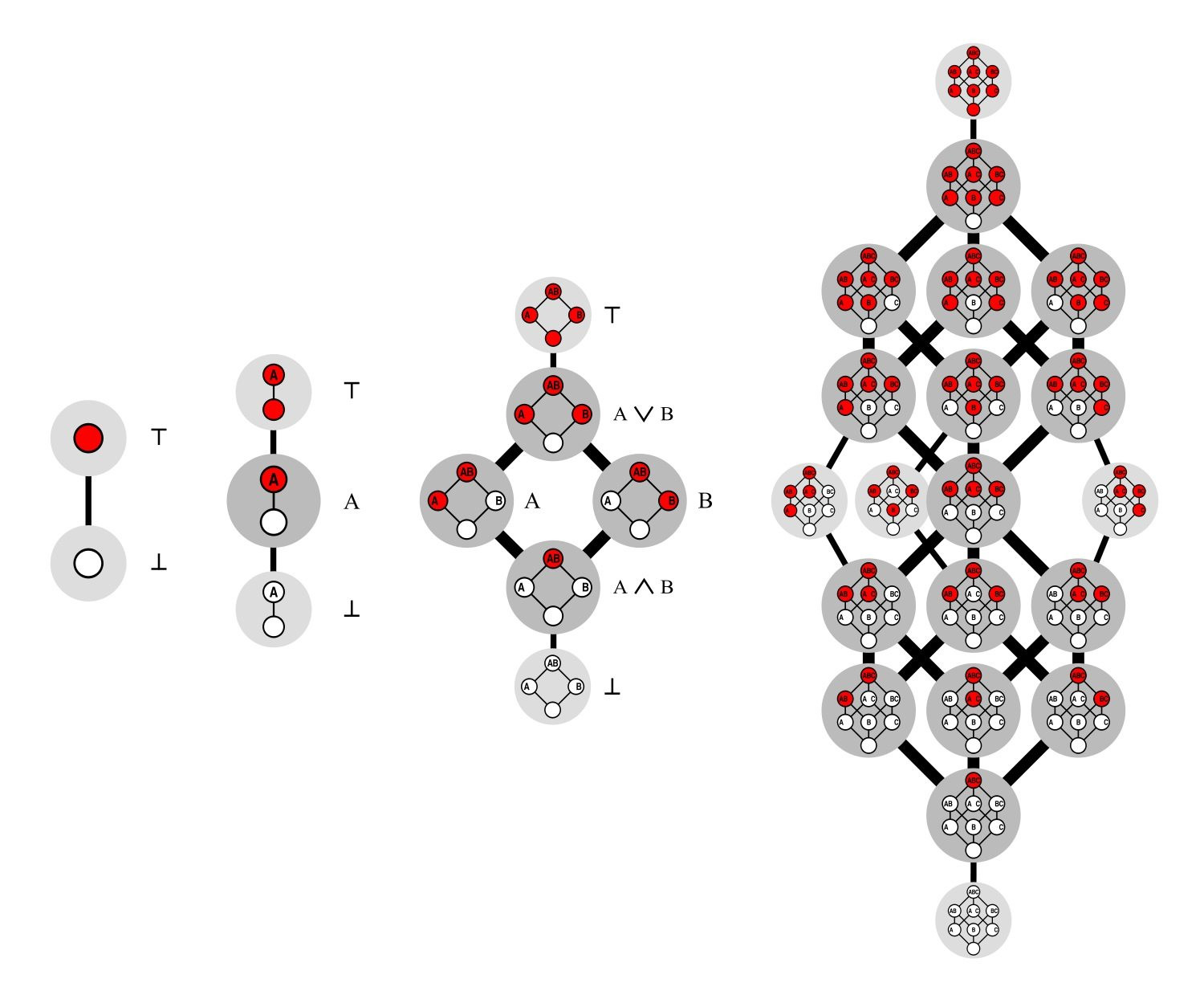
Cái gọi là các hàm Boolean đơn điệu là đối tượng chính của các số Dedekind. Theo Van Hirtum, một hàm Boolean đơn điệu trong hai, ba và vô hạn chiều giống như một trò chơi với một khối lập phương n chiều. Bạn cân bằng khối lập phương ở một góc và sau đó tô màu mỗi góc còn lại thành màu trắng hoặc màu đỏ. Chỉ có một quy tắc: bạn không bao giờ được đặt một góc màu trắng trên một góc màu đỏ. Điều này dẫn đến một loại giao điểm đỏ-trắng thẳng đứng. Mục tiêu của trò chơi là đếm xem có bao nhiêu vết cắt. Số Dedekind là những gì được định nghĩa. Con số thứ 8 đã có 23 chữ số, làm cho các con số nhanh chóng trở nên khổng lồ trong quá trình này.
Một câu chuyện cổ về việc phát minh ra trò chơi cờ vua đã truyền cảm hứng cho việc tính toán các con số tương đối lớn nhưng dễ hiểu hơn nhiều. Theo Van Hirtum, vào thời điểm này, người tạo ra trò chơi cờ vua chỉ yêu cầu nhà vua cho một vài hạt gạo trên mỗi ô của bàn cờ như một phần thưởng: một hạt trên ô đầu tiên, hai hạt trên ô thứ hai, bốn hạt trên ô thứ ba... cứ thế gấp đôi số hạt gạo trên ô sau. Nhà vua ban đầu nghĩ rằng yêu cầu này là không thể thực hiện được, nhưng sau đó nhanh chóng nhận ra rằng nó không thể thực hiện được. đơn giản vì không có nhiều gạo như vậy trên toàn thế giới. 20 chữ số, một số lượng không thể tưởng tượng được nhưng vẫn nhỏ hơn D(8), sẽ tạo nên số hạt gạo trên bảng hoàn chỉnh. Để xác định mức độ lớn của con số này, rõ ràng là cần cả một phương pháp tính toán hiệu quả và một máy tính cực nhanh để tìm ra D.
Cột mốc: Năm trở thành tháng
Các nhà khoa học đã sử dụng một phương pháp được tạo ra bởi Patrick De Causmaecker được gọi là công thức hệ số P để tính toán D. Nó cung cấp một cách để tính toán các số Dedekind, không phải bằng cách đếm mà bằng nhiều thuật toán kết hợp. Điều này cho phép D(8) được giải mã chỉ trong 8 phút trên máy tính xách tay tiêu chuẩn. Tuy nhiên, với tốc độ "8 phút", sẽ mất hàng trăm nghìn năm để D(8) được tạo ra. Van Hirtum khẳng định rằng ngay cả khi sử dụng một siêu máy tính lớn dành riêng cho nhiệm vụ này, vẫn sẽ mất nhiều năm để hoàn thành phép tính. Vấn đề cốt yếu là số lượng thuật toán trong công thức này tăng lên cực nhanh.
Theo Van Hirtum, "Trong trường hợp của chúng tôi, bằng cách khai thác tính đối xứng trong công thức, chúng tôi có thể giảm số lượng số hạng xuống "chỉ" 5,5*10*18, một lượng rất lớn. Bạn phải biết rằng có khoảng 7,5*10*18 hạt cát trên Trái đất để so sánh. Con số này cũng không quá ghê tởm. Các hoạt động trong phạm vi 5,5*10*18 khá dễ quản lý đối với siêu máy tính hiện đại, nhưng việc tính toán các thuật toán này trên bộ xử lý thông thường sẽ rất chậm và việc sử dụng GPU cho nhiều ứng dụng AI cũng không hiệu quả đối với thuật toán này.
Giải pháp: Phần cứng chuyên dụng cao, còn được gọi là FPGA, được sử dụng trong các đơn vị số học song song. Van Hirtum bắt đầu tìm kiếm một siêu máy tính có các FPGA cần thiết sau khi tạo một nguyên mẫu ban đầu cho bộ tăng tốc phần cứng. Trong quá trình này, Van Hirtum đã phát hiện ra máy tính Noctua 2 tại Trung tâm điện toán song song Paderborn (PC2) thuộc Đại học Paderborn, nơi có một trong những hệ thống FPGA mạnh nhất thế giới.
Giáo sư Tiến sĩ Christian Plessl, người đứng đầu PC2, giải thích: "Khi Lennart Van Hirtum và Patrick De Causmaeker liên hệ với chúng tôi, ngay lập tức chúng tôi sẵn lòng hỗ trợ dự án táo bạo này." Noctua 2 là một trong số ít siêu máy tính trên toàn thế giới có thể hoàn thành thử nghiệm này và giải quyết các bài toán tổ hợp khó với FPGA là một lĩnh vực đầy hứa hẹn của ứng dụng. Các yêu cầu về độ ổn định cực cao và độ tin cậy cũng đòi hỏi thử nghiệm và thách thức đối với cơ sở hạ tầng của chúng. Nhóm tư vấn chuyên gia FPGA hợp tác chặt chẽ với Van Hirtum để điều chỉnh và tối ưu hóa ứng dụng.
Sau vài năm phát triển, chương trình đã chạy trên siêu máy tính trong khoảng năm tháng. Vào thời điểm thu hoạch, các nhà nghiên cứu đã tìm thấy số Dedekind thứ 9: 28638657766829811128469151667598498 812 366.
Khi nào thì tìm ra con số Dedekind thứ 10, câu hỏi lại được đặt ra. Có số đó chắc chắn, nhưng để tính toán, cần có siêu máy tính mạnh hơn mà hiện tại con người chưa có. Tìm cách sử dụng máy tính hiện đại để tính toán cũng giống như tìm cách sử dụng tàu du hành tốc độ âm thanh để đến một hành tinh ngoài hệ Mặt trời cách xa hàng chục năm ánh sáng.
Có 8 số đầu trong dãy Dedekind: 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788.
Cập nhật tin tức công nghệ mới nhất tại fanpage Công nghệ & Cuộc sống